P=NP? P≠NP?

P 대 NP 문제에 대한 정확한 설명은 Stephen Cook 이 그의 선구적 논문 “The Complexity of Theorem‑Proving Procedures” (1971) 과 같은 시기에 러시아 학자인 Leonid Levin 논문으로 부터 출발했다. Cook-Levin 정리 발표 이후 Richard Karp가 “Reducibility Among Combinatorial Problems” (1972) 논문을 통해 21가지 문제가 NP-완전임을 증명하였다.

 

Euler diagram for P , NP , NP-complete, and NP-hard set of problems

 

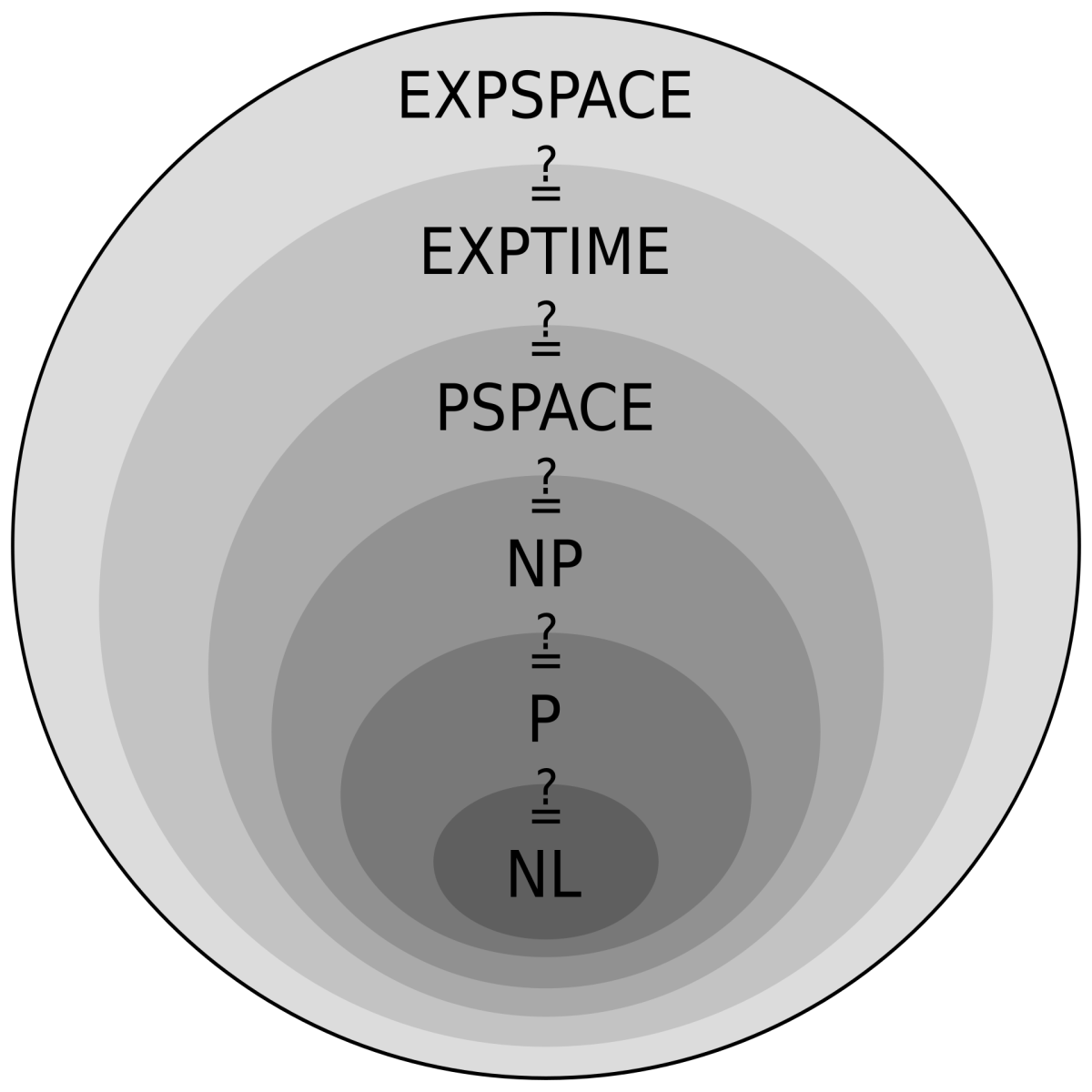
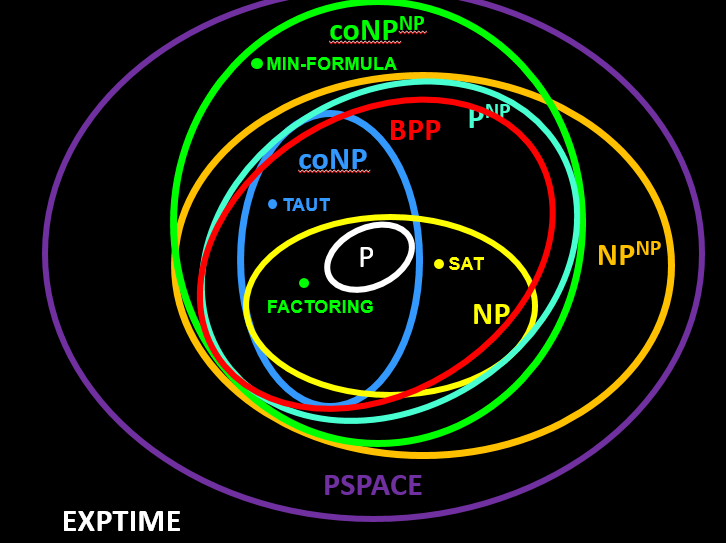
P=NP는 모든 NP 문제를 P 문제처럼 다항 시간 안에 해결할 수 있는지를 묻는 문제이다. 클래스 P는 결정론적 튜링 기계로 다항 시간 안에 해를 찾을 수 있는 문제들의 집합이고, NP는 해답이 주어졌을 때 그 해를 다항 시간 안에 검증할 수 있는 문제들의 집합이다. 따라서 P ⊆ NP는 자명하다. NP에 속하는 모든 문제는 결정론적 튜링 기계를 사용하여 부울 만족 가능성 문제(SAT)로 다항 시간 안에 환원될 수 있다. NP-완전 문제는 NP에 속하며, 동시에 NP의 모든 문제로부터 다항 시간 환원이 가능한 문제를 말한다. 따라서 하나의 NP-완전 문제에 대해 다항 시간 해법이 존재한다면, NP의 모든 문제를 다항 시간에 해결할 수 있으며, 이는 곧 P = NP 임을 의미한다. NP-hard는 모든 NP문제를 다항 시간 안에 환원 가능한 문제를 말한다.

 

복잡도 클래스 간의 관계 다이어그램